Our paper entitled “Simultaneous, cortex-wide and cellular-resolution neuronal population dynamics reveal an unbounded scaling of dimensionality with neuron number” has been published in Neuron.
The brain’s remarkable properties arise from collective activity of millions of neurons. Widespread application of dimensionality reduction to multi-neuron recordings implies that neural dynamics can be approximated by low-dimensional “latent” signals reflecting neural computations. However, what would be the biological utility of such a redundant and metabolically costly encoding scheme and what is the appropriate resolution and scale of neural recording to understand brain function?
Imaging the activity of one million neurons at cellular resolution and near-simultaneously across mouse cortex, we demonstrate an unbounded scaling of dimensionality with neuron number. While half of the neural variance lies within sixteen behavior-related dimensions, we find this unbounded scaling of dimensionality to correspond to an ever-increasing number of internal variables without immediate behavioral correlates. The activity patterns underlying these higher dimensions are fine-grained and cortex-wide, highlighting that large-scale recording is required to uncover the full neural substrates of internal and potentially cognitive processes.
It has long been argued that unraveling the dynamics of neural computation will require the ability to monitor the firing patterns of large neuronal populations distributed throughout the brain. Given the recent advancements in number of recorded units throughout the mammalian brain, dimensionality reduction has emerged as a powerful tool for visualization and interpretation of neural population dynamics. The basic underlying assumption in dimensionality reduction is that the N measured variables covary according to a smaller set of variables, often called “latent” variables in a way that the full N-dimensional state space is thought to be constrained to a lower-dimensional manifold. However, recent studies combining large-scale recording and novel unsupervised dimensionality reduction techniques suggest that the neural dimensionality of a population is higher than previously appreciated and that the observed neural dimensionality is inherited from the task or the stimulus structure.
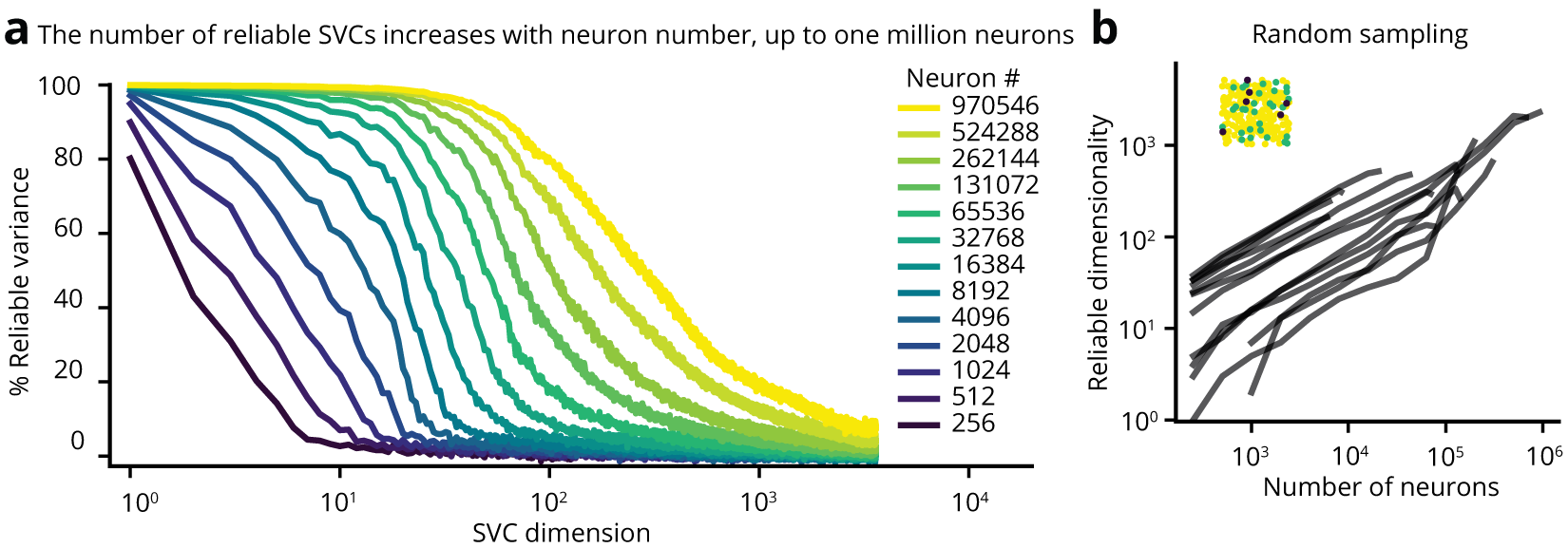
Figure 1 | Unbounded scaling of reliable neural dimensionality up to 1 million recorded neurons. (a) The dimensionality of the neuronal population as quantified by reliable Shared Variance Component (SVC) analysis exhibits unbounded scaling as a function of the number of recorded neurons up to 1 million recorded neurons. Colored traces: Different size (256 – 970,546) neural populations randomly sampled from a bi-hemispheric recorded volume with 970,546 neurons, with each trace indicating the mean percentage of reliable variance in each SVC over n=10 iterations of random sampling. Red: mean ± 95% CI for temporally shuffled data from 970,546 neurons (b) The reliable neural dimensionality exhibits unbounded scaling with neuron number. The reliable neural dimensionality is defined as the number of neural SVC dimensions with a reliable variance percentage greater than four standard deviations above the mean of corresponding temporally shuffled data. Each line indicates the mean over n=10 iterations of random sampling in a single mouse recording, ranging from 1.2 × 1.2 × 0.5 mm³ to 5.4 × 6 × 0.5 mm³ FOVs. The reliable dimensionality exhibits unbounded power law scaling as a function of the number of sampled neurons.
We hypothesized that previous observations of low-dimensional neuronal activity were the result of limitations in either the recorded population size or in accurately identifying all signal-carrying dimensions. Here we investigate this question by systematically measuring how the neural dimensionality scales with population size by recording the dynamics of up to one million neurons distributed across different depths and regions of mouse dorsal cortex using light beads microscopy (LBM) during spontaneous and uninstructed behavior in head-fixed mice. Utilizing a recent approach to identify dimensions of reliable neural variance, we demonstrated that the measured dimensionality scales according to an unbounded power law with neuron number up to one million neurons, suggesting that even at this scale of recording our technologies are still under-sampling the full state space of neural dynamics for spontaneous cortical activity (Figure 1). We identified a low-dimensional encoding of the animal’s behavior at each time point by approximately sixteen of the largest dimensions, which collectively accounted for roughly half of the observed neural variance. These behavior-related signals were encoded by multiple spatially localized clusters of covarying neurons distributed across both cortical hemispheres (Figure 2, Video 1).
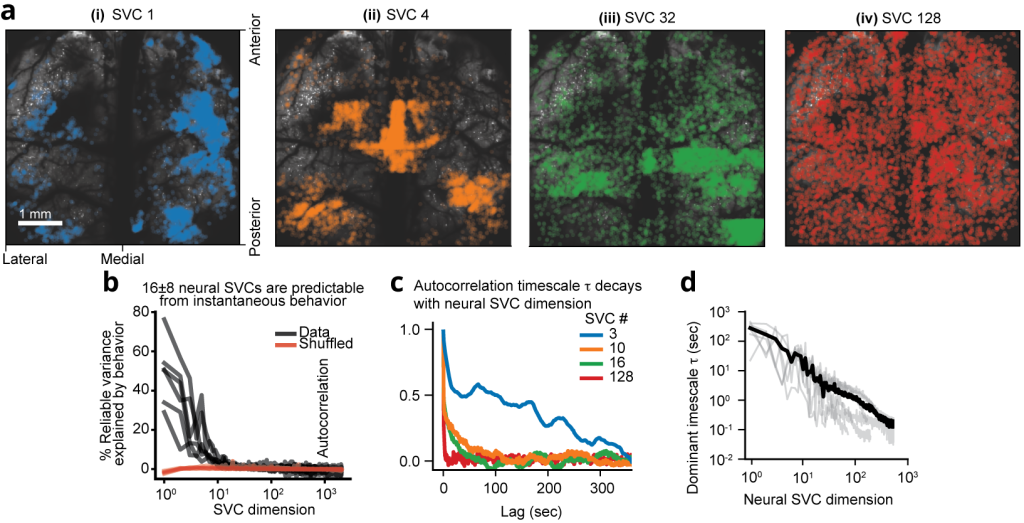
Figure 2 | Structure and geometry of low behavioral encoding versus high dimensional non-behaviorally related neuronal population activity from 1 million recorded neurons. (a) Lower and higher SVCs exhibit distinct cortex-wide neuronal distribution profiles in a bi-hemispheric recording. The spa1al distribution of the top 0.5% of neurons contributing to four example neural SVCs in a 5 × 6 × 0.5 mm³ bi-hemisphere recording with 970,546 neurons showing a wide distribution across both cortical hemispheres. (b) Only the first 16 ± 8 neural SVCs are predictable from instantaneous behavior. Using the linear, instantaneous reduced- rank regression model, the percentage of each SVC’s variance that is explained by the behavior PCs decays rapidly with SVC dimension, such that only 16 ± 8 SVCs (mean ± 95% CI, n=6 recordings with at least 131,072 neurons) show significantly more variance explained by behavior than temporally shuffled data (indicated in red, p<0.05, two-sided t-test). Each black line indicates one mouse recording. (c) Example autocorrelation curves of four neural SVCs from a recording containing 146,741 neurons. A wide variety of temporal scales are evident across all neural SVCs. (d) Characteristic timescales within each neural SVC. The autocorrelation timescale τ, computed by fitting an exponential decay to each autocorrelation curve, decays with neural SVC dimension. Gray lines show n=6 recordings with at least 131,072 neurons, black indicates their mean. Shown are neural SVCs with at least 25% reliable variance on average, which contained sufficient SNR to enable robust es1ma1on of their timescales.
Video 1 | 3D rendering of top 0.5% of neurons contributing to four example SVCs. Colors correspond to those in Figure 2a (SVC 1: blue, SVC 4: orange, SVC 32: green, SVC 128: red). Right: 3D rendering. Each dot corresponds to one neuron, and its activity is represented by its opacity. Playback sped up 10 times. Top left: Animated line plot of the temporal components of each of the plotted SVCs. Bottom left: Total animal motion energy. Note the distinct patterns of local vs. global homogeneity in the displayed SVCs.
On the other hand, given that so few neural dimensions were related to the animal’s motor activity, the observed increase in reliable dimensionality as a function of neuron number implied that the higher reliable dimensions represented neural modes without any immediate relationship to behavior (Figure 2). Nevertheless, we found that these higher-dimensional components indeed exhibited a temporal structure that is distinct from noise and spanned a continuum of timescales from seconds to the limit of the temporal resolution in our recordings (Figure 2). Given the lack of any overlap with sensory evoked neural activity, we reason that these dimensions form a high-dimensional geometry representing dynamics underlying purely internal neural computations that may enable adaptive behavior across a wide range of timescales.
While the specific nature and function of the information these signals reliably encode remains to be identified, our data highlight the potential hierarchical scales of activity spanned by cortical dynamics and suggest that such large-scale yet cellular resolution technologies provide a unique starting point to investigate how brain-wide phenomena arise from the interaction of individual neurons. Enabled by the large-scale neuronal recording capability of LBM, our results have revealed the high-dimensional geometry of spontaneous cortical dynamics and demonstrate that application of low-rank dimensionality reduction to these data would lead to loss of information, as well as systematic biases in the observed spatial profiles, timescales, and encoded features.
Relevant publication:
Jason Manley, Jeffrey Demas, Hyewon Kim, Francisca Martínez Traub, Alipasha Vaziri,
Simultaneous, cortex-wide and cellular-resolution neuronal population dynamics reveal an unbounded scaling of dimensionality with neuron number.
Neuron 112 (2024). doi:10.1016/j.neuron.2024.02.011
https://doi.org/10.1016/j.neuron.2024.02.011